Introduction to Cryptography

In this piece of note, I will give an overview of Crypotography, introduce basic principles and algorithms for symmetric cryptography, assymetric cryptography and Protocols.

Structure of Cryptography

Structure of Cryptography

Symmetric Cryptography

Same key for encryption and decryption

• Ensures confidentiality
• Implemented via block ciphers or stream ciphers
  • Lightweight and fast
  • Used for general communication

Stream Ciphers

Implementation

• Initial seed key to generate an infinite keystream of random bits

• Using same keystream to encrypt two messages -> easy to break

  • A random “number used once” ( nonce ) added as additional seed -> ensure keystream is new

• Message & keystream combined using XOR to get the cipher text

  • XOR is reversible is applied twice, which brings much convenience when decrypt cipher text.

Advantages

• Encrypting long continuous streams, possibly of unknown length
• Extremely fast with a low memory footprint, ideal for low-power devices
• If designed well, can seek to any location in the stream

Disadvantages

• The keystream must appear statistically random
• You must *never* reuse a key + nonce
• Stream ciphers do not protect the ciphertext
  • Therefore, message could be manipulated during transition without breaking confidentiality
  • E.g., suppose you are transmitting a message to bank saying A owes you $50. Attacker could either manipulate the amount or the creditor using the same stream ciper or resent the same message to server.

Block Cipers

Implementation

• Use a key to encrypt a fixed-size block of plaintext into a fixed-size block of ciphertext
  • Changing and permuting the bits of the block depending on the key
• Different lengths of messages can be handled by splitting the message up and padding

Example - SP-Networks

Wiki

• Repeated substitution and permutation

  

  SP-Network Example

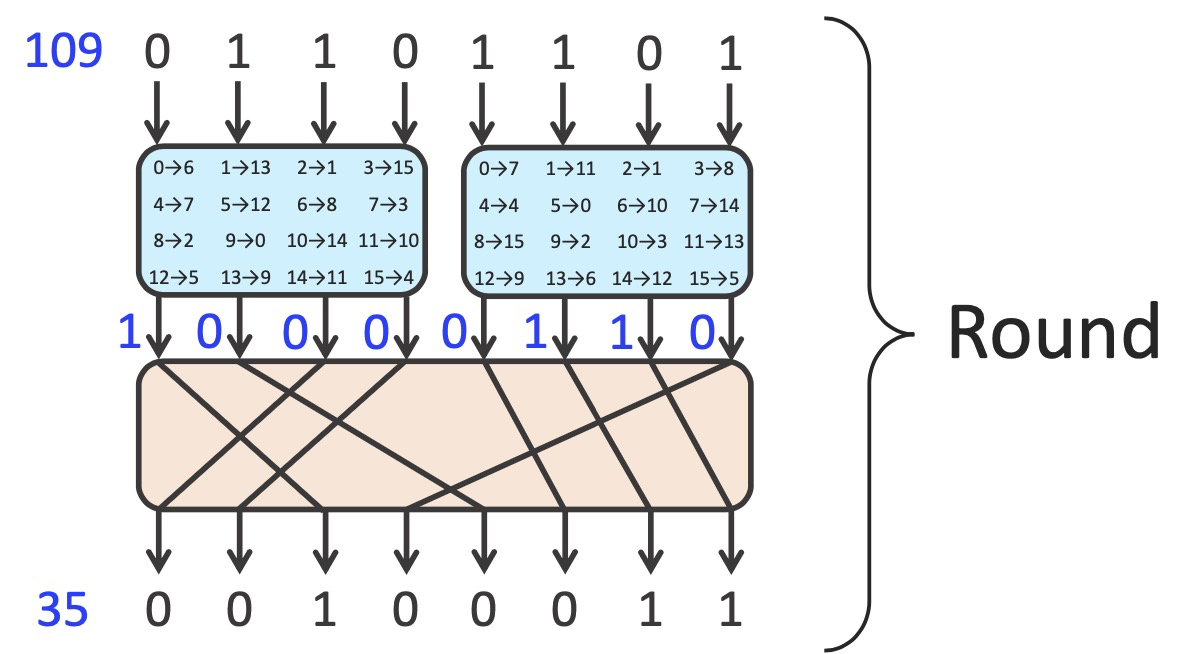
• Key mixing for enhancing security -> Different key for different round

• Decipher = Reverse operation

Symmetric Algorithms

Algorithm	Cipher Type	Design	Block Size (bits)	Speed	Memory Footprint	Safe Implementation Difficulty	Key Sizes (bits)
DES	Block	Feistel	64	Fast	Low	Easy	56
3DES	Block	Feistel	64	Slow	Low	Easy	112
AES	Block	SP-Network	128	Very fast	Low-Medium	Hard	128/192/256
ChaCha20	Stream	add-xor-rot	N/A	Very fast	Very low	Easy	256

Asymmetric Cryptography

Use a pair of keys, one public and one private

Public-key cryptography

General Idea

• Hinges upon the premise that: It is computationally infeasible to calculate a private from a public key
• In practice, it is achieved through intractable mathematical problem

Key exchange

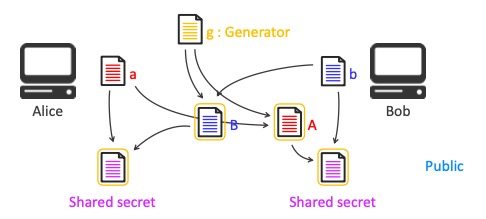
• Diffie-Hellman Key exchange allows two parties to mathematically agree a shared secret over an insecure channel

• Alice and Bob each uses a public non-reversible Generator with their private keys to generate public key and send it to each other. Using other’s public key and self’s private key, shared secret could be established.

  

  Asymmetric-Cryptography-key-exchange

Public Key Encryption

• Encryption performed by the public key can only be reversed using the private key

Digital Signatures

• The authenticity of signatures generated by the private key can by verified by the public key
• Steps
  1. Server send the original message
  2. Server use private key to encrypt
  3. Server send the encrypted message
  4. User verify using public key

Public Key Algorithms

Algorithm	Key Exchange	Encryption	Digital Signatures	Mathematical Problem	Elliptic Curves?	Typical key Size (bits)
Diffie-Hellman	✓			Discrete Logs	✓	256
RSA		✓	✓	Integer Factorisation		2048/4096
Elgamal		✓	✓	Discrete Logs	✓	2048
DSA			✓	Discrete Logs	✓	256

Protocols

Application of cryptographic algorithms in secure systems

Hash Functions

• Cryptographic primitive

• Takes a message of any length, and returns a pseudorandom hash of fixed length

• Strong hash functions

  • must appear random

  • be hard to find collisions – two messages that hash to the same thing

    

    strong hash funciton example

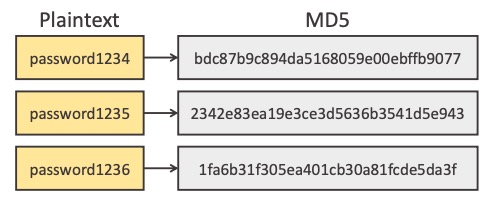
  ### Hash Function usage

Message Authentication Codes

• Provide integrity and authenticity, not confidentiality

  • Protecting system files
  • Ensuring messages haven’t been altered

• Calculate a keyed hash of the message, then append to the end of the message

  

  hash funciton in message authentication

Digital Signatures

• The use of a hash during the signing process shortens the signature
• More efficient for long messages

Password storage

• Passwords stored hashed to prevent disclosure