In this post, I will introduce the string matching problem, and a clever solution - KMP algorithm. I start from the brute force method and showed how to deduce KMP.
Introduction
String Matching Problem
- Given strings
S(lengthm) andT(lengthn), findTinS. The stringTcalled pattern. - Wide Applications, essential role in various real-world problems.
- Text processing: spell checking, text classification, information retrieval (especially in NLP field).
- Pattern recognition: bioinformatics, speech recognition
- Database management: used to searching and retrieving efficiently.
KMP algorithm
- This is an algorithm designed for the above problem, which is time efficient.
- Summary of key ideas in KMP (for those are familiar with string
matching problem):
- reduce the total comparison round --> utilize the information gained after each failed comparison
- exploit the information of the pattern string --> maintain an array for storing useful information.
Brute Force method
- Before dig into KMP algorithm, let's look at the method which
defines the lower limit of the performance.
1
2
3
4
5# Brute force algorithm for string matching
def bruteForce(S, P):
for i in range(len(S) - len(P) + 1):
if S[i : i + len(P)] == P:
print(f'Find a matching point at position {i}') # f-string1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16void bruteForce(char *s, char *p) {
int lenS = strlen(s), lenP = strlen(p);
for(int i = 0; i <= lenS - lenP; i++) {
boolean flag = true;
for int(j = 0; p[j] != '\0'; j++) {
if(s[i+j] != p[j]) {
flag = false;
break;
}
}
if(flag) printf("Find a matching point at position %d\n", i);
}
} - The intuition is pretty straight forward,
- we match the string character by character, if no failed matching till the end of the pattern string, then a successful matching was found.
- Then for the entire string, we place the pattern string at the start
of each character in
Sstring, then perform the above the step.
Analysis
- The step
1takes|P|(length of pattern string, usually marked asn) time, and the step2takes|S|(length of original string) time, we could easily conclude the time complexity is \(O(|P| \cdot |S| )\). - Why is it so slow? Or where could we improve?
- Apparently we could not optimize the comparison process at step
1, to check a match we need to perform a full comparison. - Naturally we turned to think if we could reduce the round for
matching in step
2. Look at the example below: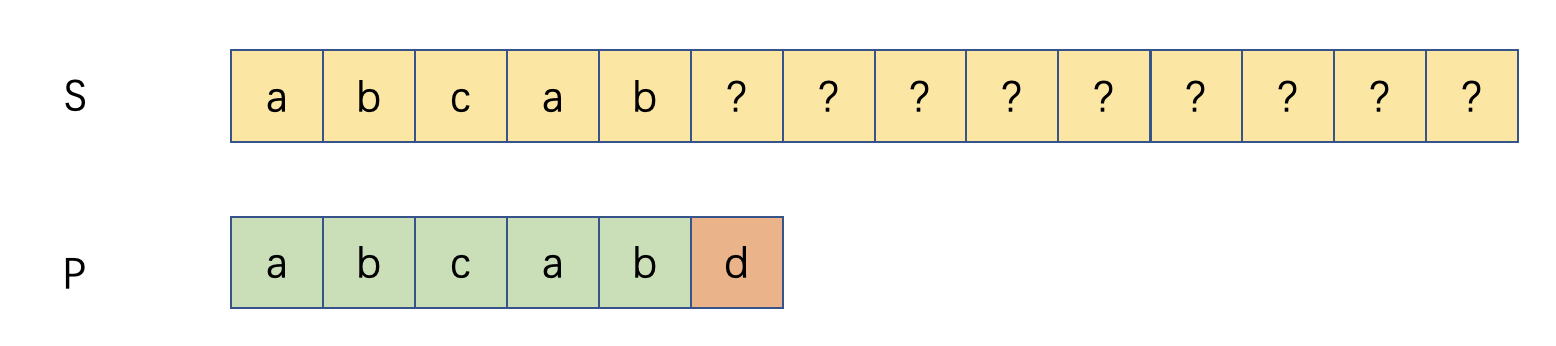
- After the above failed comparison, the brute force would start a new
round of comparison at
S[1],S[2]. These attempts is obvious to fail. The KMP algorithm therefore proposes a mechanism to skip these impossible matching. - The resulting process should be like this: (white colored means comparison skipped):
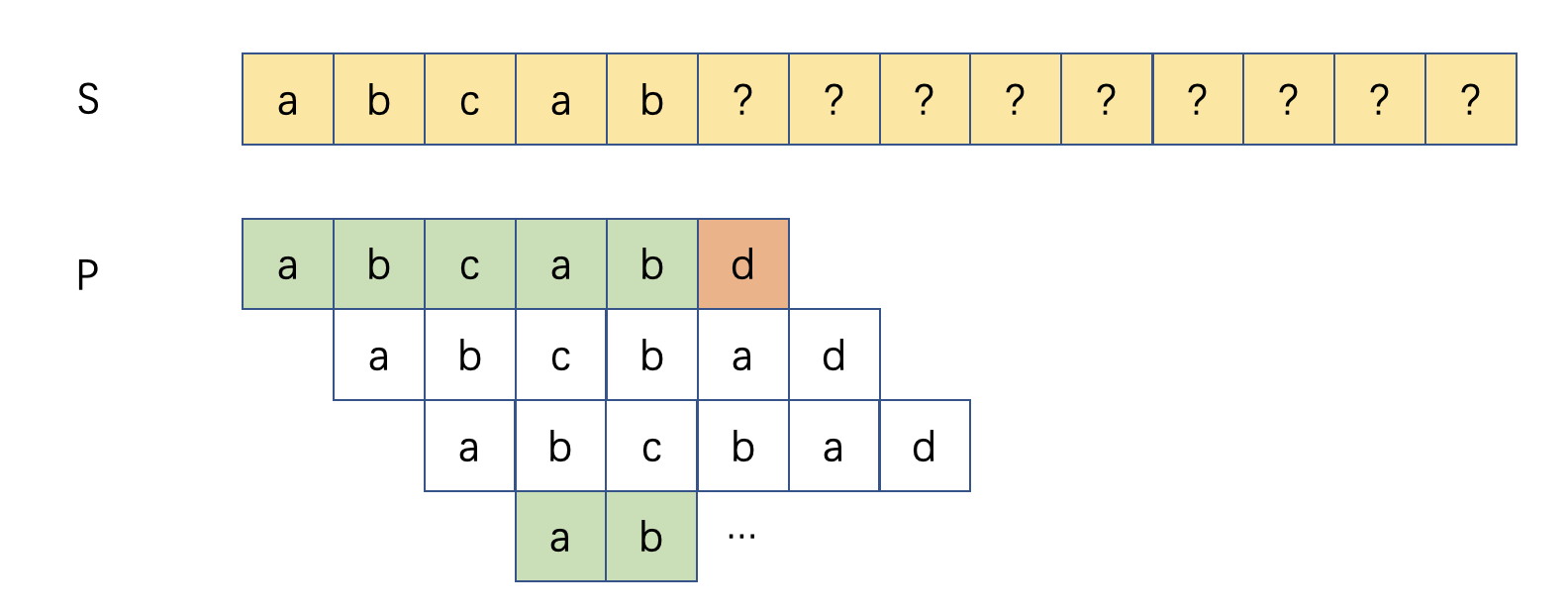
- Apparently we could not optimize the comparison process at step
Deducing the KMP algorithm
Partial Matching Table
- Following the intuition of skipping impossible
matching, we need to find a mechanism to decide which ones
should be skipped. The KMP algorithm proposed a structure called
partial matching table, which stores the information we
need.
- The partial matching table has the same length as the pattern
string, denoted as
next[]. Given the length ofPisn,next[i]represents- If substring
p[0..i]has a pair of identical prefix and suffix (p[0..k-1] == p[i-(k-1),..i]), thennext[i] = k - For example
- for the pattern string
abcabcd,we havenext[i] = [0,0,0,1,2,3,0]. Wheni = 5, the string isabcabc, therefore we could get identical pairabc, where the length is3
- for the pattern string
- If substring
- The partial matching table has the same length as the pattern
string, denoted as
- You may have noticed, with
next[]array calculated, we could skip impossible matchings by referencing thenext[]array. As shown in below example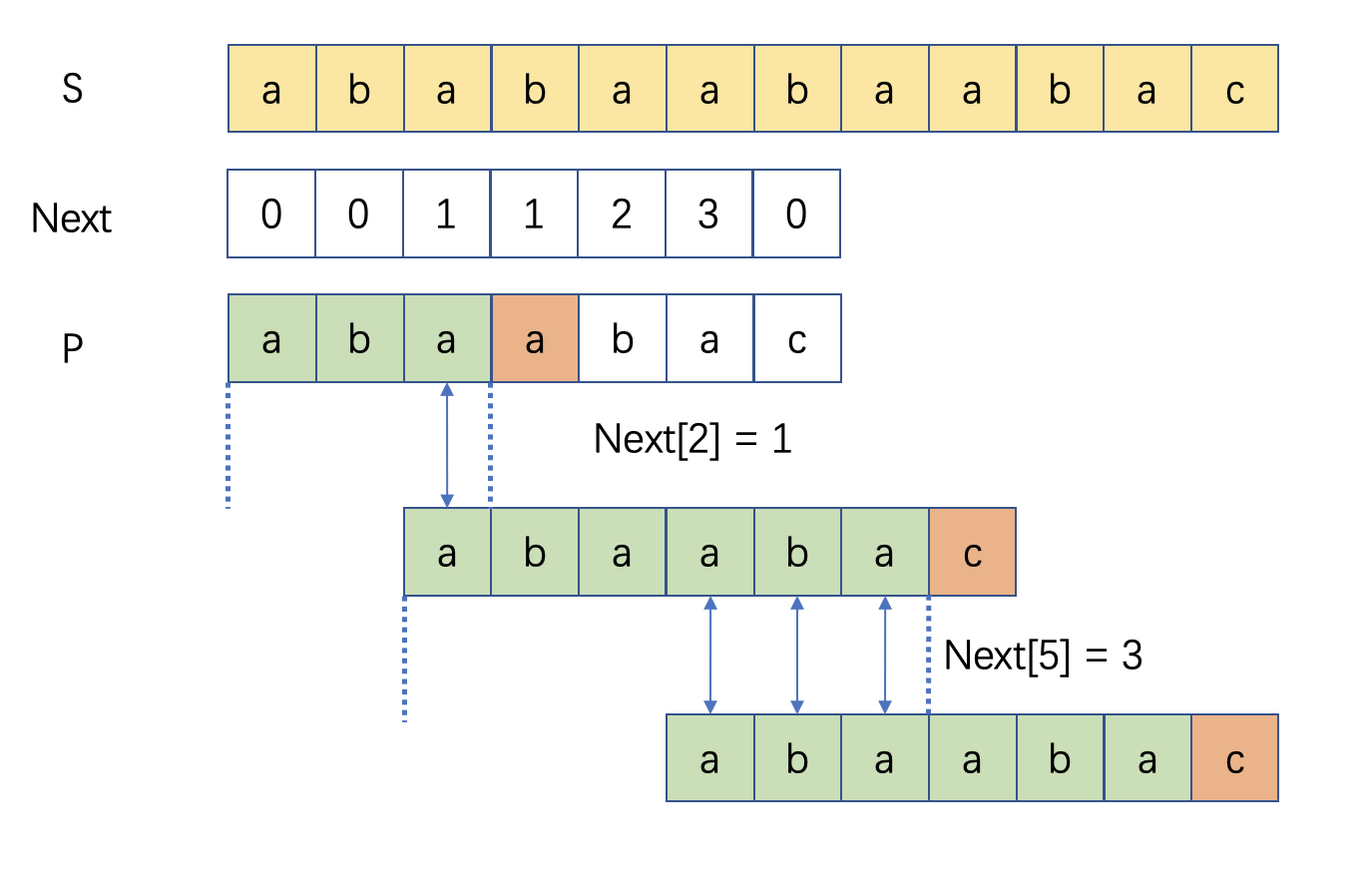
- When we failed the first match at
P[3], we replace theP[1]on the mismatched index and restart the matching. When failed the second match atP[6], we replaceP[3]on the mismatched index. - From above we could conclude, we utilize the identical prefix and
suffix for skipping some comparisons. Say the mismatch occurs at
P[i], then betweenP[0]~P[i-1], the formernext[i-1]character(s) should be the same as the latternext[i-1]character(s), so we could replace the suffix with the prefix. In conclusion, we could realignP[next[i-1]]withP[i]. - In other word, the
next[]array provides reference for how to skip comparison and how many comparison to skip.1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18# Suppose we have calculated the next[] array
def search():
s_pointer = 0
p_pointer = 0
while s_pointer < len(s):
if s[s_pointer] == p[p_pointer]: # If matched, increment both pointers
s_pointer += 1
p_pointer += 1
elif p_pointer: # mismatched at p[p_pointer], move p_pointer
p_pointer = next[p_pointer-1]
else: # mismatcher at p[0]
s_pointer += 1
if p_pointer == len(p):
print(f'The matching start point is {s_pointer - p_pointer}')
p_pointer = next[p_pointer - 1]
- How to analysis the complexity of this step?
- We could use amortized analysis, the
s_pointercould increment at mostlen(s)times, therefore the time complexity is \(O(n)\).
- We could use amortized analysis, the
Calculating Partial Matching Table
Now we have drawn the overall picture of KMP algorithm. The only problem remained is how to calculate the
next[]array.An easy way to come up with:
1
2
3
4
5
6
7def calNext(x):
for i in range(x, 0, -1):
if p[0:i] == p[x+1-i : x+1]: # Note that p[0..x] has length x+1
return i
return 0
next = [calNext(x) for x in range(len(p))]- However, the complexity of algorithm is \(O(m^2)\), as for each entry
x, we performxtimes check.
- However, the complexity of algorithm is \(O(m^2)\), as for each entry
An optimized way, consider using recursion.
- Suppose we already know
next[x-1], we want to calculatenext[x]- if
P[x] == P[next[x-1]]-->next[x] = next[x-1] + 1 - if
P[x] != P[next[x-1]]- To simply, we denote
next[x-1]aspre 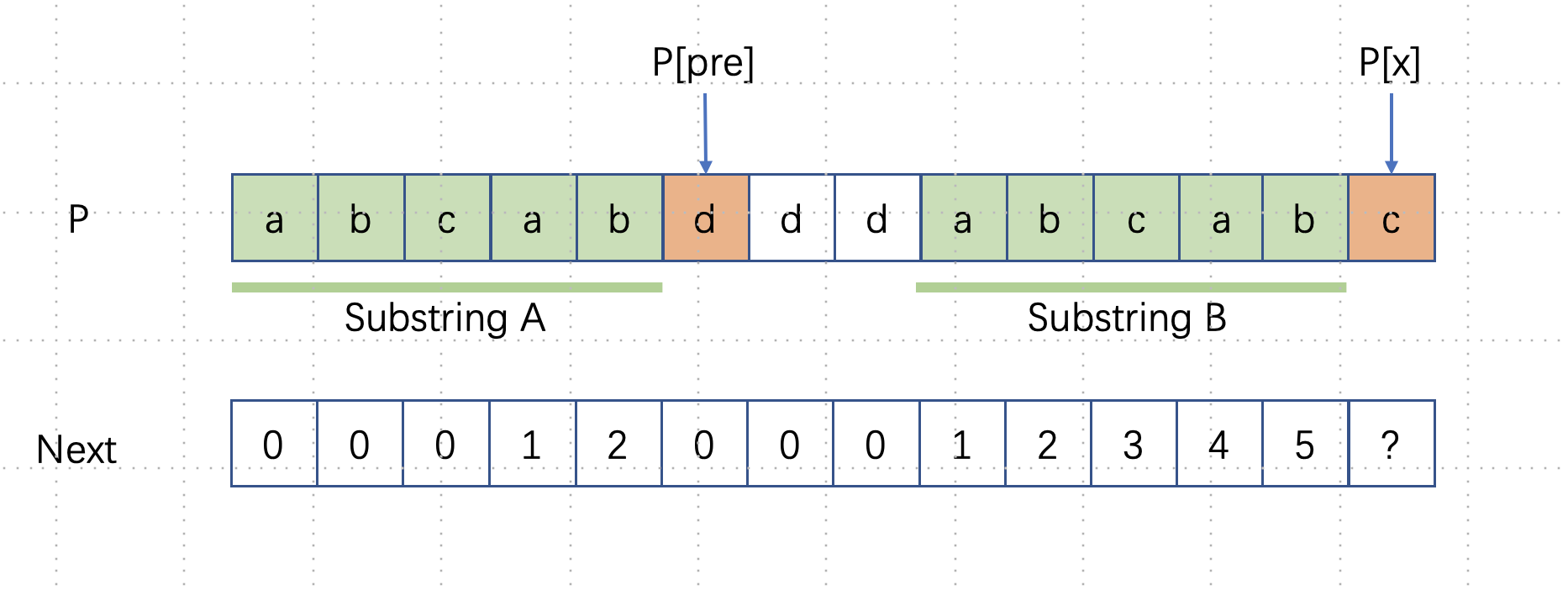
- When this two character does not match, we should shorten the
preand try the match again. We could utilize the property ofnext[]array -P[0]~P[pre - 1](A) is identical toP[x - pre] ~ P[x-1](B). - To shorten
pre, we need to find the ak, which maximizes the length, whereprefix(A,k) == suffix(B,k). - Remember
AandBis identical, then we transform the problem to find the longest common prefix and suffix ofA! which is exactlynext[pre-1]. 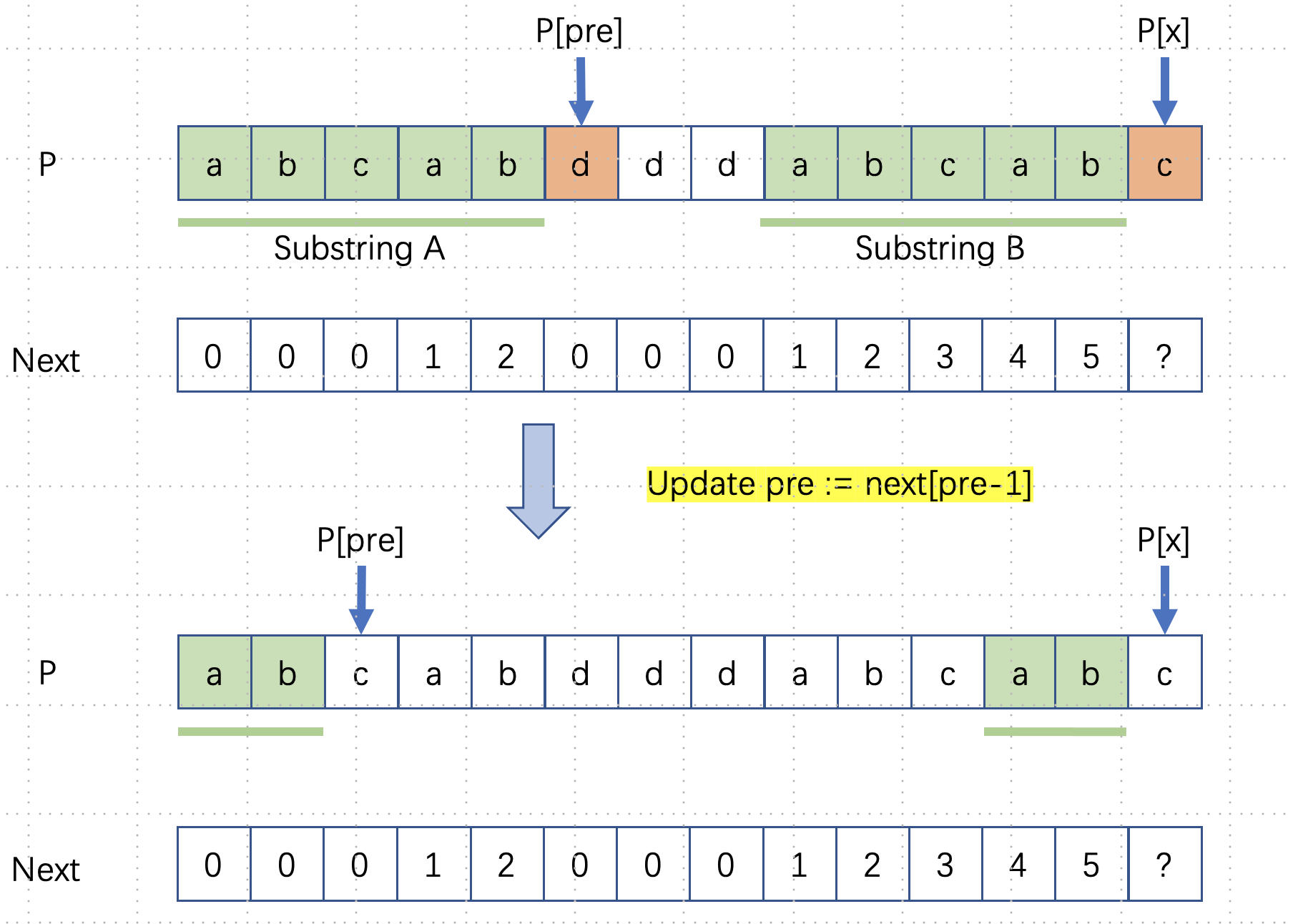
- Therefore we conclude: Iterate
pre = next[pre-1], untilP[next[x-1]] == P[x]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16next = []
def calNext():
next.append(0) # Base case
x = 1
pre = 0
while x < len(p):
if p[pre] == p[x]:
pre += 1
x += 1
elif pre:
pre = next[pre-1]
else:
next.append(0)
x += 1 - We could find the code looks similar to the one developed earlier.
It is because they actually share the same essence.
search()method perform string matching betweenSandP, wherecalNext()perform string matching betweenPandP! - Similar to previous algorithm, the time complexity is \(O(m)\).
- To simply, we denote
- if
- Suppose we already know
In conclusion, we conquer the string matching problem with time complexity \(O(m+n)\)!
Salute to the designers of this algorithm: Donald Knuth(K), James H. Morris(M), Vaughan Pratt(P).